More Resources
The procedure to use is, of course, a correlational analysis, but which type should you use? In this guide, we’ll walk you through the two main methods you could use for correlation. These methods are called the Pearson correlation and the Spearman correlation. We’ll take a look at what each technique involves, when each should be used, and the types of research questions that could be addressed. Also, if you are conducting usage and attitudes (U&A) research or concept testing, we can perform the analysis for you.
What is correlation?
Before going into detail about the statistical techniques used to perform a correlational analysis, let’s quickly define what we mean by correlation. Correlational analysis is a bivariate (two variable) statistical procedure that sets out to identify the mean value of the product of the standard scores of matched pairs of observations. The purpose of this type of analysis is to find out whether changes in one variable produce changes in another. For example, does customer satisfaction increase with the size of discount offered at a grocery store or does employee engagement rise with salary increases? Note that correlation is used to infer whether there is a relationship between the two variables, not whether changes in one variable cause changes in another. In other words, correlation says nothing about causality.
In our example above, for instance, employees might be more engaged because they're rewarded with higher salaries. Alternatively, higher levels of engagement might drive managers to increase their wages. Correlation says nothing about which variable impacts the other, but rather tells us whether there is a simple relationship between the variables, the direction of the relationship (positive or negative), and its strength.
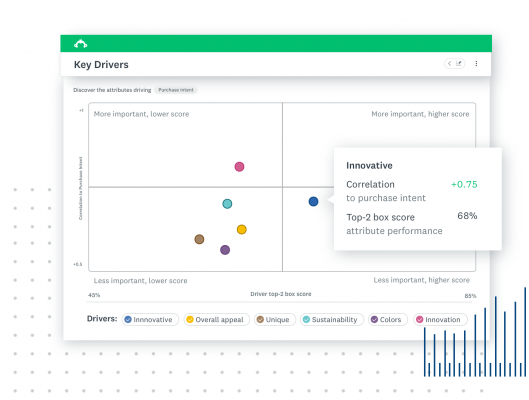
Pearson correlation method
Of two techniques used to perform correlation analysis, the Pearson correlation method is probably the most recognized and widely used in market and business research. Let’s take a look at what the Pearson correlation method is, and how you can use it.
What is the Pearson correlation coefficient?
The Pearson product moment correlation coefficient can be described as a way to measure the strength of a linear relationship between two variables—which can be used to find out if there is strong association between one variable versus another.
Imagine you have two variables—such as employee engagement and employee salaries—plotted on a simple scatter plot graph. The Pearson correlation essentially tries to utilize a scatter plot by drawing a line through the data in order to find out whether the two compariables are covary with one another and to what extent. That is, Pearson correlation coefficient identifies whether:
- There is a positive correlation between the two variables. That is, whether an increase in employee engagement is associated with an increase in salaries.
- There is a negative correlation between the two variables. More specifically, whether a rise in salaries is associated with a reduction in employee engagement, or vice versa.
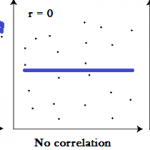
- There is no relationship between the variables. In other words, changes in salaries and employee engagement are unrelated to one another.
Insight into this relationship is a first step in understanding how variables of interest might relate to one another, and could also prompt further causal investigation.
What does the Pearson correlation coefficient test do?
The Pearson correlation coefficient test compares the mean value of the product of the standard scores of matched pairs of observations. Once performed, it yields a number that can range from -1 to +1. Positive figures are indicative of a positive correlation between the two variables, while negative values indicate a negative relationship. Furthermore, the value of r represents the strength of the relationship. A Pearson’s r that is near the value of 1 is suggestive of a stronger relationship between the two variables. As a rule of thumb, the following values can be used to determine the strength of the relationship:
- A Pearson correlation coefficient of between 0 and 0.3 (or 0 and -.03) indicates a weak relationship between the two variables
- A Pearson correlation coefficient of between 0.4 and 0.6 (or -.04 and -.06) indicates a moderate strength relationship between the two variables
- A Pearson correlation coefficient of between 0.7 and 1 (or -.07 and 1) indicates a strong relationship between the two variables.
For example, imagine that you’ve developed some marketing concepts that you’ve begun testing with some potential customers. For each concept, you’re interested in learning whether evaluations of the appeal of the concept are associated with stronger intent to purchase.
Comparisons of Concepts A, B and C yield Pearson correlation coefficients of .3 .6 and .9 respectively. Based on these three figures, you can infer the following:
- For all three market concepts, there is a positive correlation between evaluations of concept appeal and intent to purchase the purchase
- However, the correlation between concept appeal and intent to purchase is strongest for Concept C, and weakest for Concept
- For Concept B, there is positive correlation between concept appeal and purchasing intent but the relationship is moderate
Using these inferences, you might decide that Concept C is the most appropriate concept to employ in your next marketing campaign. However, first, you’ll need to determine whether the correlation you’ve observed is statistically significant. Let’s look at the formula used to determine Pearson’s r in more detail, and how you can combine this formula with a t test to determine significance.
Pearson correlation coefficient formula
The Pearson correlation coefficient coefficient (r) is calculated using the following expression:

Where xi represents the values of the x variable in a sample, x-bar indicates the mean of the values of the x variable, yi indicates the values of the y variable, and y-bar indicates the mean of the values of the y-variable. S indicates the sum of squares of the x and y variables respectively, and n is the number of observations of x and y variables.
After an r value is produced, the next step is to determine whether the value is of statistical significance. The importance of this step cannot be overstated. It is possible to observe two variables that seem to be related to one another, but the relationship is in fact meaningless.
For example, you might observe a relationship between concept appeal and intended purchase frequency, leading you to believe that the concept that has the greatest appeal will lead people to spend more. However, if this relationship occurred merely through chance, your marketing campaign might turn out to be an expensive waste of cash.
Statistical significance indicates that we are confident of a relationship between the two variables; in other words, that the result did not occur by chance.
A t test is used to establish if the Pearson’s r statistic differs significantly from zero. Statistical significance (indicated by the probability, or p) indicates whether the observer can be confident of a relationship between the two variables at different levels. For instance, a p value of .05 indicates that there is only a 5% chance that that relationship occurred by chance, while a p value of .10 indicates that there is a 10% chance that the observed correlation is a chance event.
The t statistic always has the same sign (+ or -) as the r value and is calculated as follows:
t = r* √((n-2) / (1 - r*r))
Once the t-value is calculated, it can be compared with the critical value from a standard t-table at the appropriate degrees of freedom (n-1) and the level of confidence (p value) you wish to maintain in order to determine the significance, and therefore the extent to which the correlation you have observed is meaningful.
Introducing Momentive
Learn what your audience really wants with an AI-powered solution. Shape your product and marketing strategy with our Usage and Attitudes solution.
Practical applications of the Pearson correlation coefficient
The Pearson correlation is a relatively simple equation, but its uses are myriad. You can use apply this technique to answer research questions such as:
- Is there a statistically significant relationship between age, as measured in years, and height, measured in inches?
- Is there a relationship between job satisfaction, as measured by the JSS, and income, measured in dollars?
- Is there an association between levels of household income and customer spend?
- Are higher levels of education associated with greater happiness?
Spearman correlation method
The Spearman’s test is a non-parametric version of the parametric Pearson bivariate correlation coefficient. What does this mean? Well, parametric tests and non-parametric tests are distinguished on the basis of assumptions that they make about the nature of the data to be analyzed. A parametric statistical test is a test that makes clear assumptions about the defining properties, or parameters, of the dataset. For a dataset to be appropriate for the parametric version of correlational analysis (i.e. the Pearson correlation), the following assumptions must be met:
- Each variable must be continuous in nature. In other words, each variable is able to take on a potentially infinite number of values, such as age, income or score evaluations.
- The shape of the relationship between the variables must be linear. This means that when a scatter plot of the two variables is drawn, the shape of the line of best fit should approximate a straight line rather than a curve.
If either of these assumptions are violated, you should use the nonparametric version of the correlation technique, known as Spearman’s correlation, Spearman’s rank-order test, or Spearman’s rho.
What is the Spearman correlation coefficient?
Like the Pearson test, the Spearman correlation test examines whether two variables are correlated with one another or not. The Spearman’s test can be used to analyse ordinal level, as well as continuous level data, because it uses ranks instead of assumptions of normality. This makes the Spearman correlation great for 3, 5, and 7-point likert scale questions or ordinal survey questions.
The Spearman’s test is therefore useful where the basic assumptions of linearity and continuous variables necessary to perform a Pearson's bivariate correlation analysis have not been met.
What does Spearman’s rank-order show?
The Spearman’s rank-order tests determines the strength and direction of the monotonic relationship between two variables measured at ordinal, interval or ratio level. As with the Pearson equivalent, the test will yield a figure of between -1 and +1, and the closer the figure is to 1, the stronger the monotonic relationship. As a rule of thumb, you can use the following figures to determine the effect size:
- A Spearman’s correlation coefficient of between 0 and 0.3 (or 0 and -.03) indicates a weak monotonic relationship between the two variables
- A Spearman’s correlation coefficient of between 0.4 and 0.6 (or -.04 and -.06) indicates a moderate strength monotonic relationship between the two variables
- A Spearman’s correlation coefficient of between 0.7 and 1 (or -.07 and 1) indicates a strong monotonic relationship between the two variables.
In addition, probability values should be used to determine statistical significance.
Spearman rank-order correlation formula
An example is the best way to understand how to calculate a Spearman’s correlation. Imagine you’ve gathered some data on evaluations of a market concept, and the average price a consumer is willing to pay. Take the following steps:
- In the first instance, you should create a table from your data. Each set of measurements should be ranked by assigning the ranking 1 to the largest number in a column, 2 to the next largest value, 3 to the third largest and so on (tied scores can be assigned the mean rank).
- Then, find the difference in the ranks (d). This is the difference between the ranks of the two values on each row, calculated by subtracting the ranking of the second value (in this example, price) from the rank of the first (concept evaluation).
Finally, square the differences (d2) and then sum them.
| Concept | Concept evaluation (0-10) | Concept evaluation ranking | Price willing to pay | Price willing to pay ranking | Difference between rankings (d) | d2 |
| 1 | 9 | 1 | $3.50 | 1 | 0 | 0 |
| 2 | 1 | 4 | $3.20 | 2 | 2 | 4 |
| 3 | 7 | 2 | $3.00 | 3 | -1 | 1 |
| 4 | 3 | 3 | $1.50 | 4 | -1 | 1 |
| TOTAL | 6 |
Now, you have all the data you need to calculate Spearman’s rank, using the following formula:
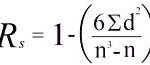
In our example, we would first multiply the sum of the d2 values (6) by 6 (i.e. 36). To address the denominator, we would raise the number of observations (concepts) to the power of 3 and then subtract the number of observations (i.e. 43-4 = 60). We can then calculate Spearman’s rho as 1-36/60= -.058. This indicates a moderate, negative monotonic correlation between concept evaluation and the price that consumers are willing to pay. A difficult one to interpret!
Practical applications of the Spearman’s correlation coefficient
The types of research questions that can be addressed through the Spearman correlation method are similar to those addressable through a Pearson analysis. Remember, however, that the main difference is that data can be ordinal in nature, and the relationship should be monotonic. For example, you could use the Spearman correlation coefficient to answer questions like:
- Is there a statistically significant relationship between participants’ level of education and their starting salary?
- Does income range vary with spend habits?
- What is the association between size of home and number of inhabitants?
Pearson Vs. Spearman correlation methods
Confused about when to use the Pearson correlation and when to use the Spearman’s correlation coefficient? Remember that Spearman's correlation determines the strength and direction of the monotonic relationship between your two variables rather than the strength and direction of the linear relationship between your two variables, which is what Pearson's correlation determines. Linear relationships are straight line relationships. Monotonic relationships differ from linear relationships in that the two variables might converge, but not at a constant rate. There are three types of monotonic functions:
- Monotonically increasing relationships
This means that as the x variable increases, the y variable never decreases.
- Monotonically decreasing relationships
This means that as the x variable increases, the y variable never increases.
- Non monotonic relationships
This means that as the x variable increases, the y variable sometimes decreases and sometimes increases.
Usage and attitudes for correlation analysis
So, that’s correlation in a nutshell, and how and when to use it. It can be complicated, but the good news is that if you’re planning on a usage and attitudes (U&A) survey or performing some concept testing, we can handle the correlation analysis for you through our Key Driver Analysis feature.
Get started with your market research
Global survey panel
Collect market research data by sending your survey to a representative sample
Research services
Get help with your market research project by working with our expert research team
Expert solutions
Test creative or product concepts using an automated approach to analysis and reporting
To read more market research resources, visit our Sitemap.
